TBI models

Linear Kelvin-Voigt (K-V) model
The well-established linear K-V model, which treats the brain matter as a viscoelastic solid with constant shear wave velocity and viscosity, is based on the following PDEs:

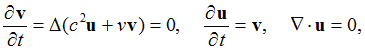
where v(x,t) and u(x,t) are the velocity and the displacement fields, respectively; c is the constant brain shear wave velocity, and v is the constant kinematic viscosity of the brain matter.
 
Nonlinear fluid model
This is our generalization of the K-V model, which treats the brain matter as an incompressible viscoelastic fluid with constant shear wave velocity and viscosity. In this model, the velocity and displacement fields are linked by means of a nonlinear material temporal derivative, i.e., the following PDEs are used:

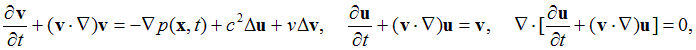
where p(x,t) is the generalized pressure that combines the fluid pressure and the hydrostatic compression term.
 
Dually-nonlinear model
This is the most general model we have developed thus far. It treats the brain matter as an incompressible viscoelastic fluid with a varying shear wave velocity c(x,t) that reflects the stiffening of the brain matter under strain and a varying viscosity v(x,t) that allows us to better emulate the gel-like properties of the brain matter:

To model the transition of distinct physical properties between the gray and the white matter as well as the flexible boundary between the white matter and the ventricles, we additionally assume that:

 
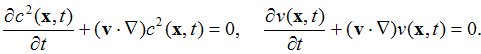
Nonlinear stress-strain model
This generalization of the K-V PDEs, which includes a varying shear wave velocity c(x,t), allows us to separately study the consequences of a nonlinear strain-stress relation and of the brain fluidity. Experimental data imply that the stress-strain relation can be approximated by c(x,t) = ce^rN(x,t), where N(x,t) is the strain norm defined below and r is a coefficient in the range [0, 2.5].

---

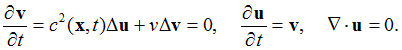
Strain Norm

The strain norm N(x,t) is the operator norm of the strain (Jacobi) matrix of the brain matter displacement U(x,t) relative to the skull, i.e.: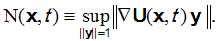
 

---

Universal Brain Injury Criterion (BIC)

Our Brain Injury Criterion generalizes the translational Head Injury Criterion (HIC) to arbitrary planar head motions. As an indicator of TBI severity, the BIC uses the maximal power transferred from the skull to the brain through narrow regions along 2D brain cross-sections. Let E(t) denote the average kinetic energy per unit mass in a thin strip of the skull's inner layer along a 2D skull cross-section at time t. Then P=|E(t₂)-E(t₁)|/T is the absolute value of the average power per unit mass in the strip during a time interval T=t₂-t₁. For an arbitrary planar head motion, the BIC formula has the form:  

where the maximum is taken over time intervals T and over all 2D cross-sections. If the final or initial head velocity is zero, the BIC formula reduces to: BIC_1000T = max(2P)^1.25T ^-0.25. For more details please see: [pdf]